I2AO Part 2: Time, Distance, Magnitude and Naming of Celestial Bodies
Back to the Index of I2AO (Introduction to Astronomy Online)
PART 2: TIME, DISTANCE, MAGNITUDE and NAMING of CELESTIAL BODIES by Lesa Moore
- Time, Universal Time & Time Zones, Sidereal Time
- Distance - Light Years and Parsecs
- Example Light Distances
- Apparent Magnitude, Intensity and Absolute Magnitude
- Names of Stars and Constellations
- Names of Other Celestial Bodies
---------------------------------
1. Time, Universal Time & Time Zones, Sidereal Time
- Astronomers use Universal Time (UT) because events (such as an eclipse) happen at a specific time, but the world has more than 24 different time zones.
- UT is virtually the same as Greewich Mean Time (GMT).
- To get local time for an astronomical event, add or subtract your time zone offset to UT.
- To convert to Australian Eastern Standard Time (AEST) use:
- AEST = UT + 10 hours
- This does not account for daylight saving so, during daylight saving (Australian Eastern Daylight Time or AEDT), you need to use AEDT = UT + 11 hours.
- Sidereal time is time as measured by the stars, rather than the Sun.
- A sidereal day is the time that it takes for Earth to spin once on its axis with respect to the stars.
- One sidereal day = 23 hours 56 minutes
- Because the Earth is also orbiting the Sun, it has to spin a little bit further than this (about an extra degree) as it goes from noon one day to noon the next day. Thus, the solar day of 24 hours is a little bit longer than a sidereal day.
2. Distance - Astronomical Units, Light Years and Parsecs
- 1 Astronomical Unit (AU) ≈ 150 million km
- One AU is the average distance between Earth and the Sun. The average distance is used because Earth's orbit is elliptical, so the actual distance varies throughout the year.
- The AU is a convenient unit for measuring distances within the Solar System.
- 1 light year (l.y.) ≈ 63,240 AU ≈ 9.46 trillion km
- A light year is the distance that light travels in a year. It is an enormous distance, but the concept is fairly easy to understand.
- Light travels at roughly 300,000 km/s. Multiply by 60 to get how far it travels in a minute, by 60 again for an hour, by 24 for a day and by 365.25 for a year.
- 1 parsec (pc) ≈ 3.2616 l.y.
- The term "parsec" stands for parallax of one second of arc.
- A parsec is the distance at which 1AU subtends an angle of one arcsecond.
- At 4.3 light years away, the nearest star to the Sun is further than 1pc away.
- Measuring parallax
- As the Earth orbits the Sun, nearby stars change their position very slightly with respect to the background stars. Surveyors use the same principle, triangulation, to measure the distance to an inaccessible object.
- You can see the effect by closing one eye and blocking out something in the distance with your thumb, using an outstretched arm. Then, without moving your thumb, arm or head, swap eyes. You should see your thumb jump to the side, revealing the previously obscured object. Now, imagine drawing a triangle with one side between your two eyes (the "baseline" of known length) and the opposite corner at the object. Angles on the diagram can be measured at the eyes, which are both aiming in slightly different directions.
- For the nearby star, the baseline is the diameter of Earth's orbit around the Sun (a known distance). The angle of interest is measured on a star chart, noting the change of position of the star between one measurement and another made six months later. With the known baseline length and the measured angle, the distance to the star can be determined using trigonometry.
- Why astronomers use parsecs
- By measuring annual stellar parallax (p), distance in parsecs (d) may be determined from the simple formula: d = 1/p
- A sample parsec calculation for Proxima Centauri appears below (reference: https://www.atnf.csiro.au/outreach/education/senior/astrophysics/astrometry1.html).
Apart from the Sun, currently the closest star to us is a small red dwarf M5 class star, Proxima Centauri. It has a parallax of 0.772". Therefore its distance is:
d = 1/p
d = 1/0.772
d = 1.30 pc
This corresponds to a distance of 4.24 light years.
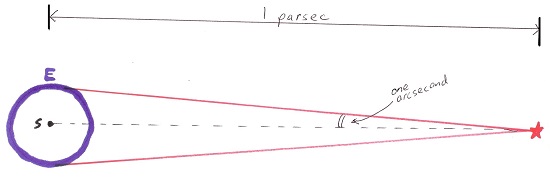
Figure 1 below: This diagram illustrates the definition of a parsec and the geometry for measuring annual stellar parallax. S is the Sun, E is the Earth, and the Earth's orbit is the purple circle. Measurements are made six months apart to get the angle between the two red lines. By definition, the baseline is 1AU (or one half-diameter of the Earth's orbit), so the half-angle (or parallactic angle), as indicated in the diagram, is used for parallax calculation. When this angle is exactly one arcsecond, the distance is one parsec. However, no star is as close to the Sun as one parsec. They are all further away, so the measured parallactic angle (or, simply, parallax) is always less than one arcsecond.
Image Credit: Diagram by Lesa Moore
- As galaxies and quasars are at very great distances, the megaparsec (one million parsecs) is a more convenient unit for distant objects.
As light travels at a finite speed, when we look at astronomical objects, we see them not as they are at this instant but as they were when the light left them. Here are some examples of light distances.
- Moon: 1.25 light seconds away
- Sun: 8 light minutes away
- Pluto: average distance from the Sun is 5.5 light hours
- Alpha Centauri: 4.3 light years away
- Milky Way: a bit over 100,000 light years across
- Distant galaxies: up to 13 billion light years away
4. Apparent Magnitude, Intensity and Absolute Magnitude
Apparent Magnitude
- Some 2000 years ago, Hipparchus devised a scheme for magnitude (m). He said that 1st magnitude stars were the brightest, 2nd magnitude were a bit fainter, down to 6th magnitude for the faintest stars that he could see with the naked eye.
- Hipparchus's magnitude scale is a scale of apparent magnitude, or apparent brightness.
- Note that the larger the (positive) number for m, the fainter the object. For very bright objects, m becomes a negative number.
- The scale has been extended in modern times to include much brighter objects, such as Venus (m = -4.5, variable) and the Sun (m = -26.72), as well as much fainter objects that may only be seen with a telescope or in long exposure photographs (e.g. very faint galaxies down to magnitude 30).
- Apparent magnitude is a function of both the intrinsic brightness of an object and the distance between the object and the observer.
- Light radiating from a star follows the “inverse square law”:
- The same star twice as far away is 1/4 as bright.
- The same star three times farther is 1/9 as bright.
- A star 100 times further away must be 10,000 times brighter to look the same
Figure 2 below: This diagram illustrates how light spreads out when it leaves a source. At double the distance, a given quantity of light is spread out over four times the area as it radiates, so the object appears only 1/4 as bright.
Image Credit: Wikipedia, Gnu Free Document License.
The following table lists the twenty brightest stars, their apparent magnitudes and their distances in light years.
| Star Name | Constellation | Apparent Magnitude |
Distance (l.y.) |
| Sun | -26.72 | ||
| Sirius | Canis Major | -1.44 | 8.6 |
| Canopus | Carina | -0.74 | 310 |
| Rigil Kentaurus (Alpha Centauri) |
Centaurus | -0.28 | 4.4 |
| Arcturus | Bootes | -0.05 | 36.7 |
| Vega | Lyra | 0.03 | 25.3 |
| Capella | Auriga | 0.08 | 42.2 |
| Rigel | Orion | 0.15 | 780 |
| Procyon | Canis Minor | 0.38 | 11.4 |
| Achernar | Eridanus | 0.45 | 144 |
| Betelgeuse | Orion | 0.50 | 430 |
| Hadar | Centaurus | 0.61 | 525 |
| Acrux | Crux | 0.74 | 320 |
| Altair | Aquila | 0.76 | 16.7 |
| Aldebaran | Taurus | 0.87 | 65 |
| Antares | Scorpius | 0.96 | 490 |
| Spica | Virgo | 0.98 | 262 |
| Pollux | Gemini | 1.15 | 33.7 |
| Fomalhaut | Piscis Austrinus | 1.16 | 25.1 |
| Deneb | Cygnus | 1.25 | 1600 |
Intensity and Intensity Ratio
- Intensity is the measure of how much light energy from a star hits a given area in a given time.
- In the modern, formal scheme, stars that differ by 5 magnitudes have an intensity ratio of exactly 100.
- Therefore, one magnitude difference is an intensity ratio of 100 raised to the power of 1/5, or 2.512.
- The intensity-ratio sequence for a range of five magnitudes is approximately 1, 2.5, 6.3, 16, 40, 100.
Absolute Magnitude
To compare the properties of different stars, it is useful to standardise their magnitudes to how bright they would appear if they were all at an equal distance. This derived magnitude is absolute magnitude (M).
- Absolute magnitude may be thought of as how bright a star really is.
- Absolute magnitude is defined as the star’s apparent visual magnitude if it were at a distance of 10 pc.
- The table below compares magnitudes of Sirius, a nearby middle-sized star, and Rigel, a distant giant. Sirius is the (apparently) brightest star in the night sky. It is bright because it is close to us. Rigel is fainter in apparent magnitude but is really a much bigger, brighter star seen from a long way away.
| Star | App Mag (m) | Distance | Abs Mag (M) |
| Sirius | -1.44 | 8.6 l.y. | +1.4 |
| Rigel | -0.15 | 780 l.y. | -7.1 |
- Rigel is really two-and-a-half thousand times brighter than Sirius (eight-and-a-half magnitudes brighter in absolute magnitude).
Further detail is provided here: How Astronomers Measure Distances.
For those who are interested, or have some background in mathematics, some maths for "Intensity ratio and magnitude difference" and "Distance modulus and distance" are available here.
5. Names of Stars and Constellations
CONSTELLATIONS
- Many of the constellation names we use today were given to them in antiquity, as recorded by Ptolemy in 150 A.D. This applies to those observable from northern latitudes – the stars that were visible from what we now call Europe, Britain, the Middle East and Egypt.
- New constellations were added in the 17th and 19th centuries by Johann Bayer, Johannes Hevelius and Nicolas Louis de Lacaille. Inspired by what the explorers had seen when they travelled south of the equator, some southern constellations were named after exotic birds (such as the toucan and the bird of paradise) and others were named after the navigational instruments essential for mapping and finding the way back home (the compasses, the level, the sextant and so on).
- As well as adding new constellations, modern astronomers rearranged Argo Navis, a very large constellation of Ptolemy's. It has been broken up into four separate constellations, Carina, Puppis, Vela and Pyxis.
- Finally, the constellation boundaries were formalised by the International Astronomical Union in 1930, which was when a portion of Ophiuchus was assigned to cross the ecliptic, making it the 13th "sign of the zodiac".
- The convention is that Latin words are used for constellation names. Two-part constellation names start with a noun, followed by an adjective (in the Latin genitive case). The ending of the adjective has to do with the gender of the noun, often an inanimate object! Compare the constellations Corona Australis, Triangulum Australe and Piscis Austrinus. Australis, australe and austrinus all mean "southern" but the endings differ because the crown (corona) is feminine, the triangle (triangulum) is neuter and the fish (piscis) is masculine.
- Today, western culture recognises 88 constellations in the sky, each with a 3-letter abbreviation.
- e.g. CMa (Canis Major), Sgr (Sagittarius), Psc (Pisces), CrA (Corona Australis)
STARS
- Proper names are used for the brightest stars (those known to the ancients).
- e.g. Sirius (Greek), Altair (Arabic), Regulus (Latin)
- The convention of using a Greek letter with Latin constellation name was introduced by Johann Bayer in 1603.
- Bright stars in the constellations are given Greek letter designations, starting with alpha for the brightest star, beta for the second-brightest and so on. For example, Alpha Canis Majoris is the brightest star in the constellation of Canis Major (and also has the proper name, Sirius).
- Most of the stars in Argo Navis kept their original Greek designations so, consequently, Puppis and Vela have no star designated alpha or beta and Carina has no gamma or delta.
- The whole star name uses the Greek letter plus the Latin constellation name but, when combined, the constellation part takes the Latin genitive case. For example, in the constellation Centaurus, we have the well-known star alpha Centauri, meaning "alpha of Centaurus". For star names, the genitives give variations like alpha Gruis (in Grus), delta Crucis (in Crux) and theta Scorpii (in Scorpius). Sometimes the adjective changes (alpha Canis Majoris in Canis Major), sometimes it is the noun (alpha Coronae Australis) or sometimes both (alpha Trianguli Australis).
- Greek symbols are used on star charts.
- Faint stars may have only a catalogue number (catalogues will be discussed in a later online module).
A full list of constellation names, genitives, meanings and abbreviations is available on Wikipedia here: https://en.wikipedia.org/wiki/88_modern_constellations
6. Names of Other Celestial Bodies
- Minor bodies (asteroids and comets) get an alpha-numeric designation. A letter indicates comet (C for a comet on an escape orbit, P for a periodic comet) or asteroid (A), year, letter for half-month, letter for order of discovery in half-month.
- Comet P/1983 V1 (Hartley-IRAS) is a periodic (P) comet, discovered in 1983 in the second half of November (V = 22nd half-month) and was the first (1) discovered in that half-month, found by Malcolm Hartley and the IRAS survey. Comets are the only objects named after their discoverer.
- Asteroids may be named by their discoverer after some other person.
- Supernovae (expoloding stars) are named SN, year and letter for order of appearance.
- e.g. SN1987A was the first supernova of 1987.
- Craters on the Moon are named after scientists and astronomers.
- e.g. Copernicus, Eratosthenes, Kepler, Tycho, Newton
Figure 3 below: This photo shows craters on the Moon. The craters are most easily seen along the terminator (the line between the sunlit area and the area in darkness). The term "crater" was first used by Galileo. In his telescope, he saw these cup-shaped depressions and named them after crater, the Greek word for cup.
Image Credit: Photo courtesy Ángel Rafael López-Sánchez.
Author: Lesa Moore, 26th July 2017. Minor revisions 28th January 2018.