Astronomy through the Ages - Prehistory to ancient Greece and Rome
Back to the Index of I2AO (Introduction to Astronomy Online)
| Next |
ASTRONOMY THROUGH THE AGES: Prehistory to Ancient Greece and Rome by Lesa Moore and Ian Kemp
- c. 4500 BCE – Nabta Playa
- c. 500 BCE – Pythagoras
- c. 400 BCE – Plato
- c. 350 BCE – Aristotle
- c. 310 BCE to c. 230 BCE – Aristarchus of Samos
- c. 276 BCE to c. 195 BCE – Eratosthenes of Cyrene
- c. 150 CE – Ptolemy
- c. 355 CE to 415 CE – Hypatia
-----------------------
1: c. 4500 BCE – Nabta Playa
Author: Lesa Moore
How do you know when spring is coming? Or your birthday, for that matter. We take our calendar for granted these days. It was a little more challenging 6500 years ago.
Nabta Playa is a natural depression, with an area of about 5000 square km, west of the Nile River in what is today southern Egypt. It lies close to the Tropic of Cancer. It appears that by about 6500 years ago, inhabitants at Nabta Playa had developed a sophisticated, accurate way of marking time and the seasons, using the Sun and stars.
They constructed a stone circle and other monuments. According to researchers, there were alignments to Arcturus, Sirius and alpha Centauri. Some stones align with north and others indicate the direction of sunrise on the day of the summer solstice. The latter marked the approach of the summer rainy season, when there was enough water in the playas for large groups and their animals. Whilst the stones are not so massive (note the scale bar in the second image below), these sites predate Stonehenge by at least 1000 years.
Of course, the climate has changed since then, so you'll be waiting a long time for the summer rains!
Figure 1.1 below - Nabta Playa Sites: Diagram of the Nabta Playa sites.
Image Credit: Nature 392, 488-491 - Megaliths and Neolithic astronomy in southern Egypt (Malville et al., 1998), permission through Rightslink. 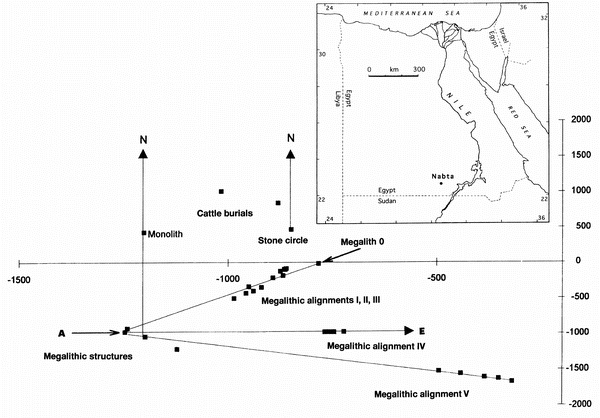
Figure 1.2 below - The Stone Circle: Discovery images and diagram of original stone placements.
Image Credit: Nature 392, 488-491 - Megaliths and Neolithic astronomy in southern Egypt (Malville et al., 1998), permission through Rightslink. 
Figure 1.3 below - The full circle: A more recent photo (c. 2007) of the Nabta Playa stone circle.
Image Credit: Wikimedia Commons

2: c. 500 BCE – Pythagoras!
Author: Ian Kemp
The right-angled triangle guy! Yes, but this famous ancient Greek expert on ‘The Immortal Soul’ and religious ritual, was possibly much more than that, or possibly not event that. So far as we know, Pythagoras actually wrote nothing at all during his life (570 BCE to 490 BCE), but writings about him and the knowledge attributed to him grew after his death. His ideas on cosmology would be barely recognised today, being based on the idea that the cosmos was structured according to moral principles (for example, the planets were meant to be instruments of divine vengeance), but he was interested in numerology and numerical patterns in the heavens, and later workers might have thought he was on to something with his ideas about the ‘music of the spheres’, especially when the ratios of the planetary orbits were discovered centuries later.
Unfortunately, the earliest evidence that links him with the famous theorem, and with his astronomical findings, was written about 1000 years after his death but, if not due to him, these ideas most likely came from his followers (his ‘school’). In terms of astronomy, the two main findings attributed back to him that we care about today are:
- Spherical bodies: Pythagoras supposedly deduced that the Moon was spherical, as the only possible explanation for the curved shape of the terminator (the division between dark and light when the Moon is partially sunlit). This is actually quite a significant logical deduction, given that most people who have not been schooled in the matter find it difficult to explain even the phases of the Moon. Applying the theory of the time he reasoned that all other astronomical bodies should be the same. Later observers backed this up with the observation of the curved shadow of Earth during a lunar eclipse, together with other Earth-bound evidence.
- Venus: Attributed to Pythagoras is the realisation that the Morning Star and the Evening Star were, in fact, a single body - the planet Venus. Such a shame that very little of the written history of the era has survived for us.
Figure 2.1 below - Bust of Pythagoras (Capitoline Museum)
Image Credit: Wikimedia Commons

Figure 2.2 below - The changing shape of the lunar terminator
Image Credit: Fred Espenak

Figure 2.3 below - Coin Issued under Joint Reign of Valerian and Gallienus: (reverse) Pythagoras with Globe
Image Credit: Institute for the Study of the Ancient World

3: c. 400 BCE - Plato
Author: Lesa Moore
Let’s think about this.
Plato was known as a great philosopher, and one of the reasons why he is so famous is that his written works have survived for over 2400 years. Whilst not an astronomer, nor truly a mathematician, he was known to have been a teacher of mathematics and is said to have been influenced by Pythagoras. His philosophical discourses also touch on the origin of the world, which he attributed to a “Demiurge” (the most highly placed of the gods) who made order from the jumble of matter. From Plato’s text, “Timaeus”, he appreciates that the heavenly bodies mark out time: the fixed stars divide the night from the day, the Moon marks the months and the Sun describes the year. He also sees these heavenly bodies as divine, and considers that time itself came into being with their celestial movements.
Did he understand orbits? Though not explicitly stated by Plato, it seems from his discussion that he saw the Earth as the centre of the Universe, with the other heavenly bodies in orbit around it. He inherited the view that the circle or sphere was the most perfect of geometric shapes and was, therefore, appropriate for the Earth and the cosmos. It was generally accepted at this time that orbits were perfect circles.
Figure 3.1 below - Statue of Plato in Athens
Image Credit: Photo by Lesa Moore

4. 350 BCE - Aristotle
Author: Ian Kemp
According to one of today’s leading lights in physics, Sean Carroll, Aristotle “was no dummy”. Well, that’s faint praise for a philosopher who learned all he could from the genius, Plato, and became recognised as such a know-it-all in so many subject areas that we coined a special word in the English language: Aristotelian. He only lived for 62 years (384 BCE to 322 BCE), but his ideas continued as the mainstream in ‘science’ for hundreds of years, and were still the mainstay of physics in Newton’s day (the 1600s), so Aristotle’s ideas held sway for about 1800 years. Which is quite odd, because they are so obviously wrong, and can be disproved by some quite simple observations.
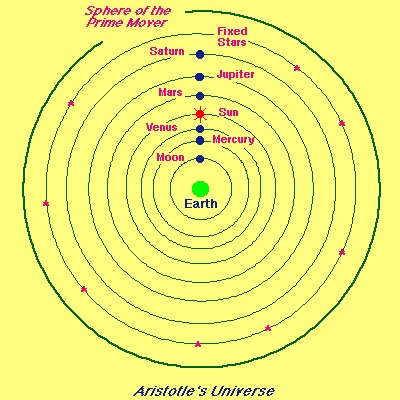
Aristotle’s mistake (I can smirk because I’m a visitor from the long distant future!) was his belief in Statics - his philosophy was that things would naturally remain the same, unless some violent action made them change. This type of thinking is easily disproved by observation but, for over a thousand years, people preferred the authority of the classics to the evidence of their own eyes. Today, of course, we think that the natural state of things is dynamic, i.e., change, and the type of change can be computed using general relativity or quantum mechanics. Despite my deprecation of Aristotle, he is known as the first philosopher to recommend learning by empirical observation - collect data and reason from it. Based on the weak and inaccurate naked-eye observations of the time, he championed the spherical Earth, at the centre of the Universe, surrounded by a large number of ‘crystalline spheres’ on which the planets turn. His ideas on the structure of the universe were bung but, at a deeper level, his ideas on how knowledge should progress were key in the development of science for millennia, up to and including today. Having said this, his incorrect ideas, uninformed by observation, held sway until the Middle Ages, in a society mostly interested in paying homage to ‘ancient wisdom’.
Figure 4.1 below - Bust of Aristotle
Image Credit: Encyclopedia Britannica

Figure 4.2 below - Aristotle’s solution to the solar system: In this diagram, the planets are aligned for convenience. The outermost sphere was the domain of the “Prime Mover”. The Prime Mover caused the outermost sphere to rotate at constant angular velocity, and this motion was imparted from sphere to sphere, thus causing the whole thing to rotate. This system did not explain the varying brightness of the planets, nor retrograde motion.
Image Credit: Eric G. Blackman (http://www.pas.rochester.edu/~blackman/ast104/aristotle8.html)
5: c. 310 BCE to c. 230 BCE – Aristarchus of Samos
Author: Lesa Moore
Thanks to Archimedes, we know that Aristarchus believed that “the fixed stars and the sun remain unmoved, that the earth revolves about the sun on the circumference of a circle, the sun lying in the middle of the orbit”. He placed the Sun at the centre of the Universe, with the Earth and other planets orbiting in circles around the “central fire”.
Furthermore, he thought that stars were just like our Sun, but really far away. This wasn’t Aristarchus’s own idea, but was suggested earlier by Anaxagoras. Unfortunately, his ideas didn’t hit it off because (a) we, on Earth, have no sense that we are moving through space and (b) if the Earth were moving around the Sun, star positions should change relative to each other as Earth moves around its circle. On this last point, I’ll mention that other references will cite parallax as the problem (parallax in stars is only measurable where you have stars at different distances). But, if you recall from Aristotle, the belief at the time was that the stars were all on a giant crystal sphere, meaning that there should be no expectation to observe parallax, only the change in the separation of the stars as Earth came closer and further away. So, this is a huge exaggeration, but imagine you’re on a merry-go-round – the spectators appear well-separated and far apart when you see them up close, whereas they appear closer together, in angular terms, when they’re on the far side. This effect was not observed - hence, Aristarchus’s opinion that the stars were so very far away that you wouldn’t be able see the effect. Others just thought he was wrong.
One work by Aristarchus survives, “On the Sizes and Distances”. Noted, in his day, for his mathematical ability, Aristarchus did some geometry and made calculations of the relative distances to the Sun and Moon, concluding that “the Sun was between 18 and 20 times farther away than the Moon.” The modern-day ratio is that the Sun is 400 times farther than the Moon, but he was on the right track.
Imagine the discussions these guys must have had, arguing back and forth as to which was the correct model of the Universe – geocentric or heliocentric. And it would have been way less confusing if so many clever ancient Greeks didn’t all have names starting with “A”!
Figure 5.1 below - Sculpture of Aristarchus
Image Credit: Russell Cottrell

Figure 5.2 below - Aristarchus’s heliocentric model
Image Credit: Rob Hollow, CSIRO
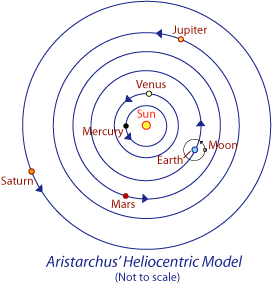
Figure 5.3 below - Copy of Aristarchus's work: A 10th century CE Greek copy of Aristarchus of Samos’s 2nd century BCE calculations of the relative sizes of the Sun, Moon and the Earth.
Image Credit: Vat. gr. 204 fol. 116 recto math06 NS.02, Public Domain.

6: c. 276 BCE to c. 195 BCE – Eratosthenes of Cyrene
Author: Lesa Moore
Ever thought about your dream job? Eratosthenes was a librarian at the Great Library of Alexandria! He had the opportunity to do lots of reading. One day, he read an account from Syene (some distance to the south of Alexandria) of how, on 21st June (the longest day of the year), at exactly midday, columns cast no shadow and sunlight passed straight to the bottom of a well. Eratosthenes did the experiment. In Alexandria, he measured the angle of the Sun’s shadow on 21st June and found it to be seven degrees. Interesting!
He reasoned that the only way this was possible was if the surface of the Earth were curved – consistent with earlier views about the Earth being a sphere. But he didn’t stop there. He determined that seven degrees was 1/50th of a full circle. All he needed was to work out the distance between Alexandria and Syene, multiply by 50, and he would have a measurement of the circumference of the Earth. By some means, the measurement and calculation were made. The separation between the cities was found to be 5000 stadia or 800 km, implying that the circumference of Earth was 250,000 stadia or 40,000 kilometres. Today, we determine it to be 40,075 km.
Is that awesome, or what! I should probably also mention that he invented geography and mapped the known world at the time (c. 194 BCE), with positions of 400 cities.
Figure 6.1 below - Eratosthenes’ Experiment: This simple demonstration with cardboard and straws shows the effect that Eratosthenes measured.
Image Credit: Photo by Lesa Moore (after demo by Carl Sagan).

Figure 6.2 below - Eratosthenes' Geometry: The ratio of the shadow’s angle to a full circle is the same as the ratio of the separation between the two cities to the full circumference of Earth.
Image Credit: Wikimedia Commons

Figure 6.3 below - Eratosthenes’ portrait
Image Credit: Public Domain

7: c. 150 CE – Ptolemy
Author: Ian Kemp
For those smarties (like me) who criticise the Aristotelian cosmology, because it can’t cope with retrograde motion, the Ancient Greeks had an answer. Now, epicycles may not have been invented by Ptolemy, but they are associated with his name because of The Book. The Great Book. The Majestic Book, al Magest. Written in the second century CE by Claudius Ptolemy (100-170), this publication was a summation of all that was known and thought (mostly thought, rather than known) about the Universe at the time … and for a long time after; the Arabic rendition of the title is because the book was the standard textbook on astronomy for about 1400 years. In fact, you can still order your copy today on Amazon (https://www.amazon.com.au/Ptolemys-Almagest-Ptolemy/dp/0691002606) or the Book Depository (https://www.bookdepository.com/Ptolemys-Almagest-Ptolemy/9780691002606).
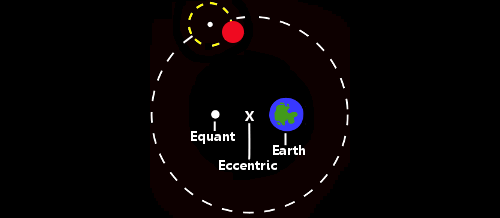
I wouldn’t recommend reading it if you are after a degree in physics or a post-grad degree in astronomy but, as an exercise in logic and the history of science, it is really something. The retrograde motion of Jupiter and Saturn are explained by having the planets fixed, not to a crystalline sphere, but to something that rotates around a point on the crystalline sphere. Thus, circling a point in empty space, the planets can be more easily made to follow the tracks seen in the sky. Of course, there is no explanation of why the epicycles should exist, what binds them to the deferent (the main orbit) or why the great creator should have made such a mess, but that doesn’t matter when your credibility is based on your reputation rather than the power of your predictions.
But, despite its theoretical dodginess, al Magest was the go-to reference guide for the medieval astronomer. Compiled in the city of Alexandria, it omitted some of our well-loved southern constellations, but was based around a catalogue of over 1000 stars including their relative brightnesses. I have, in fact, done Ptolemy a disservice, because his cosmology included a thing called the ‘equant’, which was able to explain away most of the errors that the circular-orbit theory makes when trying to predict planetary motion. For more info, see Amazon or Book Depository (links above)!
Little known side fact: Hard-core fans of British writer, Terry Pratchett, call him “Pterry”. Probably due to his naming one of his characters “Ptraci”, an obvious hat-tip to our 2nd-century hero of the day.
Figure 7.1 below - Ptolemy idolised in medieval times
Image Credit: SPL (free use)

Figure 7.2 below - Ptolemy’s cosmology
Image Credit: Doug Stewart
8: c. 355 CE to 415 CE – Hypatia
Author: Lesa Moore
In 30 BCE, Alexandria (established in 331 BCE by Alexander the Great) made the transition from being part of the Hellenistic world to being part of the Roman empire. It is famed for its library, part or most of which had burnt in 48 BCE. The surviving texts of the ancient Greeks were written predominantly by men (as far as I am aware). However, at least one woman did have the opportunity to indulge in intellectual pursuits. It may have helped that her father was a respected mathematician. Hypatia was a Hellenistic Neoplatonist philosopher who also taught mathematics and astronomy. She is the first female mathematician whose life was well recorded.
She wrote commentaries on Diophantus’s “Arithmetica” and on Apollonius of Perga's treatise on conic sections. The latter has not survived and the former was apparently interwoven with the original text.
She succeeded Theon as head of the Platonic school and she served as a trusted advisor to the city’s leaders, including its governor, Orestes. I won’t go into the politics of religion, only to say that her life was taken too soon.
The conic sections, for those not familiar, are the various ways of cutting a cone to produce one of these geometric shapes: a circle (horizontal); a parabola (parallel to the slope of the cone); an ellipse (any cut between the angles of the circle and the parabola) or a hyperbola (beyond the angle of the parabola, intersecting both the upright and inverted cones).
Hypatia’s character has been dramatized in the movie “Agora”, where she is seen in her home town of Alexandria teaching scholars from around the Mediterranean. In the movie, she is attributed with coming up with the idea that the orbit of Earth around the Sun may be an ellipse, rather than a circle. This is based on apparent observations of the Sun where observers of her time have, supposedly, noted a change in the apparent diameter of the Sun between aphelion and perihelion. Would the ancients have been able to discern the 3.4% difference? Or is this just dramatic licence? I’ll let you decide.
Figure 8.1 below - Hypatia: No extant original images or sculptures exist.
Image Credit: This illustration is from “A Short Animated Introduction to Hypatia, Ancient Alexandria’s Great Female Philosopher”.

Figure 8.2 below - The conic sections
Image Credit: Lumen Learning

| Next |

